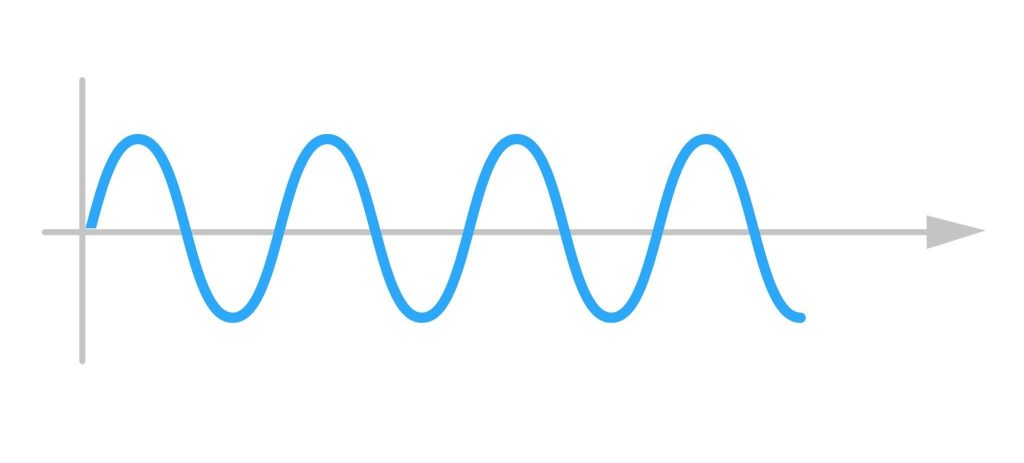
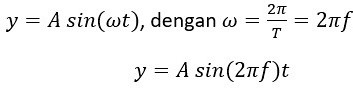Dalam ilmu sains, kita mengenal beberapa macam getaran. Salah satunya ada yang disebut sebagai getaran harmonis. Lalu apa pengertiannya? Jadi, getaran harmonis adalah gerakan sebuah benda secara bolak – balik atau periodik melalui titik keseimbangan.
Gerakan pada getaran harmonis disebut juga sebagai gerak osilasi. Suatu getaran disebut sebagai getaran harmonis jika memiliki ciri tertentu. Apa saja ciri yang dimaksud?
Daftar isi
Ciri – Ciri
Berikut beberapa ciri yang perlu kamu ketahui sebagai dasar mempelajari getaran harmonis:
- Gerakan yang terjadi pada getaran harmonis berupa gerakan yang sifatnya bolak – balik
- Getaran harmonis timbul akibat gerakan yang secara periodik terus berulang
- Titik keseimbangan berada di bagian tengah lintasan dan pasti dilewati oleh gerakan tersebut
- Percepatan yang bekerja pada sebuah getaran harmonis sebanding dengan simpangan benda
- Arah percepatan yang bekerja pada suatu getaran harmonis selalu menuju ke arah titik keseimbangannya.
Contoh Benda yang Menghasilkan Getaran Harmonis
Beberapa benda yang ada di sekitar kita mampu menghasilkan getaran harmonis, di antaranya:
- Bunyi dawai pada alat musik
- Gelombang radio
- Arus listrik pada AC
- Denyut jantung manusia
Galileo Galilei yang merupakan seorang astronom, filsuf dan fisikawan dari Italia bahkan disebut – sebut sudah mengetahui getaran harmonis ini dari beberapa puluh tahun silam. Bahkan bapak ilmu fisika modern ini diduga telah menggunakan denyut jantungnya sendiri untuk mengukur waktu dalam pengamatan gerak.
Pada getaran harmonis, periode dan frekuensi getarannya dapat dihitung untuk mendapatkan informasi periode dan frekuensi secara secara dengan sebuah rumus. Berikut penjelasannya!
Periode dan Frekuensi Getaran Harmonis
Getaran dapat menghasilkan gerakan, terlebih jika frekuensinya berulang – ulang dan dalam periode yang cukup panjang. Nah, penjelasan tentang periode dan frekuensi nyatanya dapat dihitung dan diukur.
Kali ini akan kita ukur dengan didasarkan pada periode dan frekuensi pada acuan sistem pegas dan bandul sederhana.
Periode dan frekuensi pada sistem pegas
Dalam ilmu fisika, setiap getaran dapat menghasilkan gerak. Nah, getaran harmonis dapat menghasilkan gerak harmonik. Apa yang dimaksud dengan gerak harmonik?
Gerak harmonik merupakan suatu gerak melingkar beraturan yang terdapat pada salah satu sumbu utama benda yang mengakibatkan gerak. Periode dan frekuensi terjadinya gerakan tersebut bisa dihitung dengan menyamakan antara gaya pemulih (F = -kX) dan gaya sentripental (F = -4π 2 mf2X).
Pada sistem beban pegas, periode dan frekuensinya hanya bergantung atas massa dan juga konstanta gaya pegas.
Periode dan frekuensi pada bandul sederhana
Pada bandul sederhana, suatu bandul terdiri atas beban dengan massa (m) yang digantung pada ujung tali ringan (sehingga massanya diabaikan) dengan panjang 1. Jika beban ditarik pada satu sisi dan kemudian dilepaskan, maka beban berayun akan memiliki suatu titik keseimbangan menuju ke sisi yang lainnya.
Jika amplitudo ayunannya kecil, bandul akan melakukan getaran harmonik dimana periode dan frekuensi getaran harmonik yang terjadi pada bandul sederhana akan sama dengan frekuensi getaran yang terjadi pada pegas.
Itu artinya bahwa periode dan frekuensi getaran pada bandul sederhana dapat dihitung dengan menyamakan antara gaya pemulih dan gaya sentripentalnya.
Adapun persamaan gaya pemulih pada bandul sederhana adalah F = -mg sinθ. Dimana sudut θ kecil (θ dalam satuan radian) maka sin θ = θ. Sehingga persamaannya ditulis dengan rumus F = -mg (X/1) karena persamaan gaya sentripentalnya adalah F = -4π 2 mf2X.
Pada bandul sederhana, periode dan frekuensinya tidak bergantung pada massa dan simpangan bandul melainkan hanya bergantung pada panjang tali dan juga percepatan gravitasi tempat bandul berada.
Karakteristik Gerak Harmonik pada Bandul Sederhana dan Getaran Pegas
Gerak Harmonik pada bandul sederhana dan getaran pegas memiliki ciri atau karakteristik berikut ini :
Simpangan
Simpangan merupakan jarak benda dari titik keseimbangan yang bisa dibuktikan dengan rumus persamaan berikut :
Kecepatan
Rumus kecepatan pada getaran harmonis adalah :
v = A ω . cos . ω t
Kecepatan maksimum pada getaran harmonis dapat diperoleh, jika nilai ω t = 0.
Karenanya dapat disimpulkan bahwa Vmaks = ω t
Percepatan
Percepatan pada getaran harmonis adalah perubahan kecepatan yang didasarkan pada satuan waktu. Persamaannya sebagai berikut :
Atau secara sederhana, persamaannya sebagai berikut :
Gaya pemulih
Gaya pemulih merupakan suatu gaya yang dimiliki benda elastis sehingga dapat kembali pada bentuk semula. Persamaannya yaitu :
F = -k. x
F : lambang atau simbol gaya pemulih
K : lambang atau simbol konstanta pegas
x : lambang atau simbol pergeseran ujung pegas dari posisi keseimbangan.
Contoh Soal Getaran Harmonis Dalam Pelajaran Fisika di Sekolah
Suatu benda bergetar dan membentuk suatu gerak harmonis dengan persamaan sebagai berikut :
y = 0,04 sin 20π t
Diketahui y adalah simpangan dalam satuan meter, t adalah satuan waktu dalam sekon (second). Tentukan berapa besaran dari persamaan getaran harmonis di atas :
- amplitude
- frekuensi
- periode
- simpangan maksimum
- simpangan saat t = 1/60 sekon
- simpangan ketika sudut fasenya berada di 45 derajad
- sudut fase ketika simpangannya berada di rentang 0,02 meter
Jawab :
y = A sin ωt
ω = 2π f
atau
ω = 2π/T
maka,
1. Amplitude atau A
y = 0,04 sin 20π t
↓
A = 0,04 meter
2. Frekuensi atau f
y = 0,04 sin 20π t
↓
ω = 20π
2πf = 20π
sehingga f = 10 Hz
3. Periode atau T
T = 1/f
maka T = 1/10 = 0,1 s
4. Simpangan maksimum atau ymaks, sehingga
y = A sin ωt
y = ymaks sin ωt
y = 0,04 sin 20π t
↓
y = ymaks sin ωt
ymaks = 0,04 m
Note : Simpangan maksimum juga disebut sebagai amplitudo. Jadi jika ada soal mencari amplitudo maka cara perhitungannya sama seperti perhitungan bagian jawaban (d) ini
5. Simpangan saat t = 1/60 sekon
y = 0,04 sin 20π t
y = 0,04 sin 20π (1/60)
y = 0,04 sin 1/3 π
y = 0,04 sin 60° = 0,04 × 1/2√3
maka y = 0,02 √3 m
6. Simpangan saat sudut fasenya 45 derajad
y = A sin ωt
y = A sin θ
dimana θ adalah sudut fase, θ = ωt
y = 0,04 sin θ
y = 0,04 sin 45° = 0,04 (0,5√2)
maka y = 0,02√2 m
7. Sudut fase ketika simpangannya berada di rentang 0,02 meter
y = 0,04 sin 20π t
y = 0,04 sin θ
0,02 = 0,04 sin θ
sin θ = 1/2
maka θ = 30°
Kesimpulan
Getaran harmonis adalah getaran bolak – balik yang bersifat periodik dan sangat bermanfaat bagi manusia. Cukup banyak benda di sekitar kita yang dapat menjadi contoh getaran harmonis dan tentu sangat berkaitan erat dengan kehidupan manusia.